A simple and practical way to best select tasks to finish

This is a light post, but practical and easy to implement, to improve our productivity in prioritising tasks.

Very common we have problems selecting which task we should do first within a limited time or resource to meet a specific deadline, such as a project milestone meeting, submission of purchase of an equipment or conference paper submission.

Instead of using a quantitative and systematic manner, we tend to select tasks to finish subjectively and by intuition.

For a small number of tasks, this way of selecting task by intuition may work. However, when we have many tasks from which we need to select to finish first, this selection by intuition may cause sub-optimal task selections.

Sub-optimal task selections mean that we select tasks that may use a lot of time or resources but have minimal impacts to the whole project we need to finish or to the significance of the task delivery at that time.

Let’s go into the discussion.

READ MORE: Research how to: A practical guide

Do you want to have good research philosophies and improve your research management and productivity?

This book is a humble effort to map well-known and proven principles and rules from various disciplines, such as management, organization decision theory, leadership, strategy, finance and marketing, into a single practical research guide that applies to all disciplines.

You can also get this book from Rakuten Kobo.

Task selection as a min-max problem

When we have many tasks to do with different importance levels and required resources, we can model this problem as ”min-max” optimisation problem [1].

That is, the “min-max” optimisation problem describes an optimisation problem when we want to maximise return or profit (in this case finishing the most important tasks) while at the same time we want to minimise cost or lost (in this case resource required to finish the tasks).

In mathematical form, we can describe the problem as:

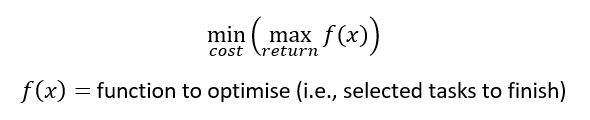
To solve this problem, one way is we can solve the optimisation sequentially. That is, first we maximise tasks that give the most return (those that have the highest level of importance) and then minimise (select) the tasks based on those who require minimal resource (such as time to finish or cost).

Practical and easy guidelines to optimise “min-max” optimisation problem

• For criteria that we want to maximise (e.g., importance), we need to sort by “Largest to smallest (Descending order)”.
• If there are multiple criteria to maximise (e.g., performance and safety), we need to sort from the least importances to the most importance criteria in “Largest to smallest (Descending order)”
• For criteria that we want to minimise (e.g., cost), we need to sort by “Smallest to largest (Ascending order)”.
• If there are multiple criteria to minimise (e.g., cost and labour time), similarly, we need to sort from the least importances to the most importance in “Smallest to largest (Ascending order)”

In the next section we will discuss two examples to shade light or give clarity on this “min-max” problem and on the implementation of the practical guidelines to solve the “min-max” problem of prioritising tasks.

READ MORE: Reverse step: building research and knowledge from data or observation study

Examples for optimal task selections

In this example, we use a problem where we have a list of tasks to finish. Each task has different levels of “importance” (factor to maximise) and levels of “required resource” (factor to minimise, such as time or cost)

There are two examples derived from the same task list. The first one is a simple task selection where we want to select the most importance tasks while minimising time required to finish the tasks.

The second one is the extension of the first problem. This second problem we expand the factor to maximise into “performance” and “safety”, and the factor to minimise into “cost” and “time to finish”.

In the two examples below, we use a hypothetical task list related to a project that require a software and hardware development, software-hardware integration, testing and data analysis.

The total number of tasks we need to select (prioritise) are 10 tasks. Each task has different levels of factor to maximise and different levels of factor to minimise.

Suppose we have a milestone deadline within < 24 hrs and we need to finish tasks that have the most importance level to optimise the impact of our progress within the given 24 hrs.

Each factor has level from 1 to 5. Level 1 means that the factor is the least important or the least required cost and level 5 means the highest importance or the highest required cost.

Example 1: Task selection with one factor to maximise and minimise

In this example, we have only one factor to optimise, that is “importance” and one factor to minimise, that is “required time to finish”.

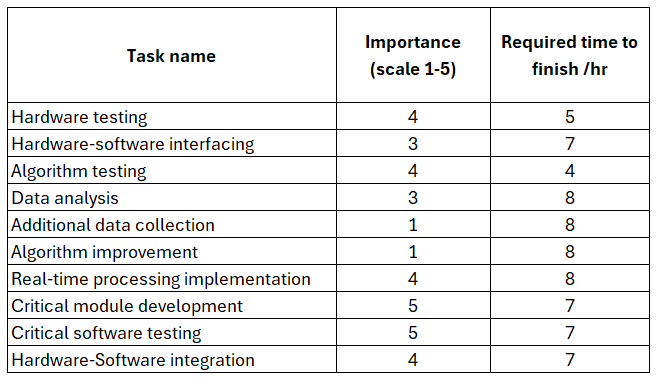
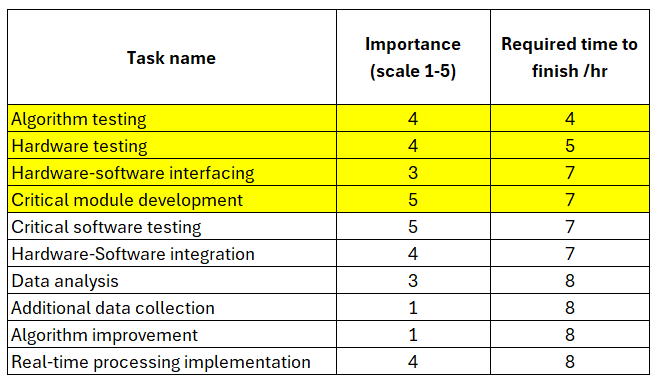
Table 1 below shows the list of the task to be selected so that we can deliver the highest impact on the project milestone meetings within < 24 hrs.

Table 2 and table 3 below shows the results of the selected task when we follow the quantitative guidelines to solve the “min-max” task selection problem and when we directly only select based on tasks that require the least time to finish, respectively.

Table 2 is obtained by first, sort the task list based on “importance” column from largest to smallest (Descending order) and then re-sort the table based on “required time to finish” column from smallest to largest (Ascending order).

Based on table 2, the selected tasks are algorithm testing, hardware testing, critical module development and critical software testing.

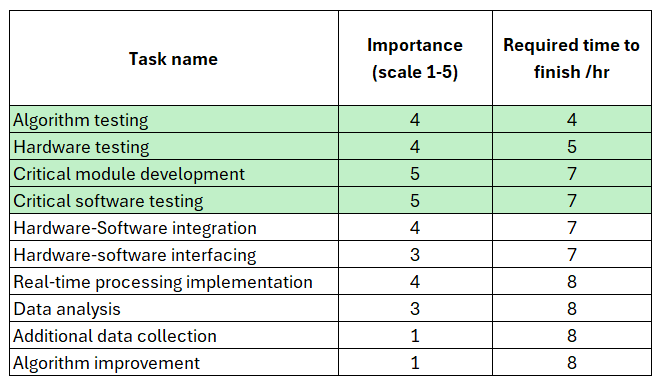
Meanwhile, table 3 is obtained by directly sort the task based on the “required time to finish” column from the smallest to the largest.

Based on table 3, The selected tasks are algorithm testing, hardware testing, hardware-software interfacing and critical module development.

Clearly, we can see the different for the selected tasks between table 2 and table 3.

Since table 2 follow the simple and practical guide to quantitively solve the “min-max” task selection problem, the selected task from table 2 select the tasks that have the highest importance level within the given < 24 hrs.

Example 2: Task selection with two factors (with different priority) to maximise and minimise

In this example, we expand the previous example by adding more criteria to be maximised and minimised.

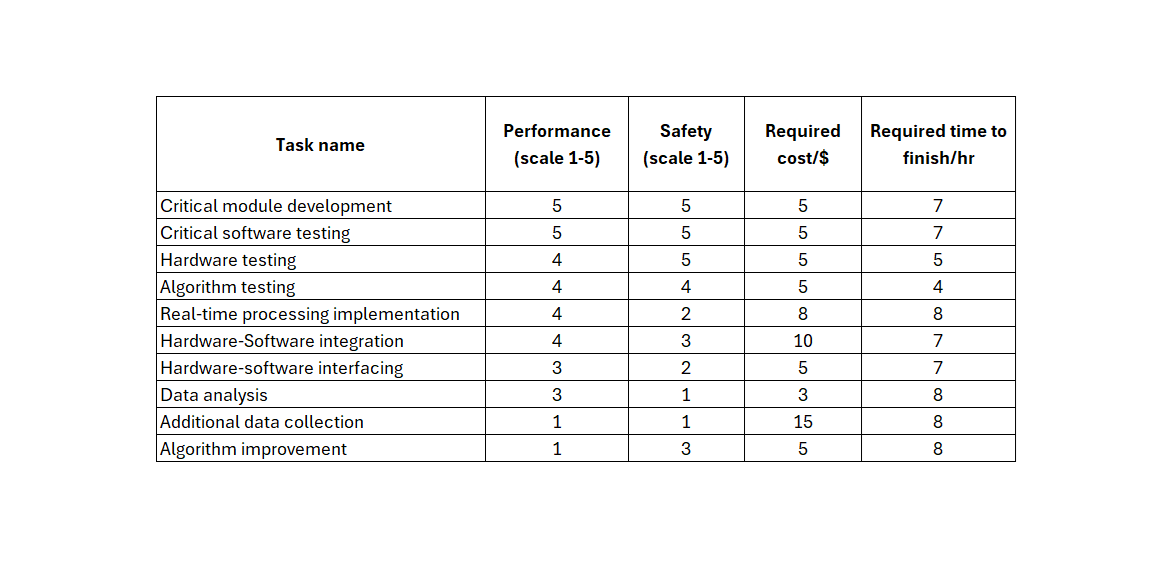
In this example, the criteria to be maximised are “performance” and “safety” of the product that our project is going to make. The “safety” has a higher priority than “performance”.

Meanwhile, the criteria to be minimised are “required cost” and “required time to finish” for each task. The “required time to finish” has a higher priority than “cost”.

Regarding determining the criteria to maximise or minimise, we can follow the concept of “simple rule” by Prof. Eisenhardt [2].

Based on this rule, we must determine criteria by only a few and the criteria should be easy to remember.

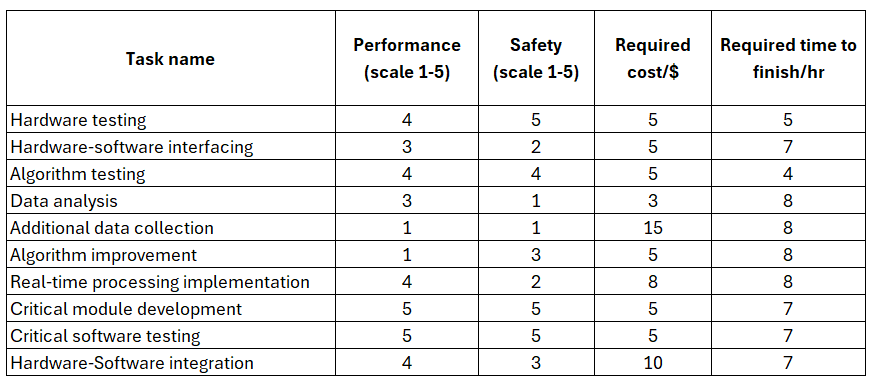
Table 4 below shows the task list to be selected when we have the multiple criteria to maximise and minimise.

Table 5 and table 6 show the result of selected tasks by implementing the “min-max” optimisation procedure and by directly select the task with the least required time to finish, respectively.

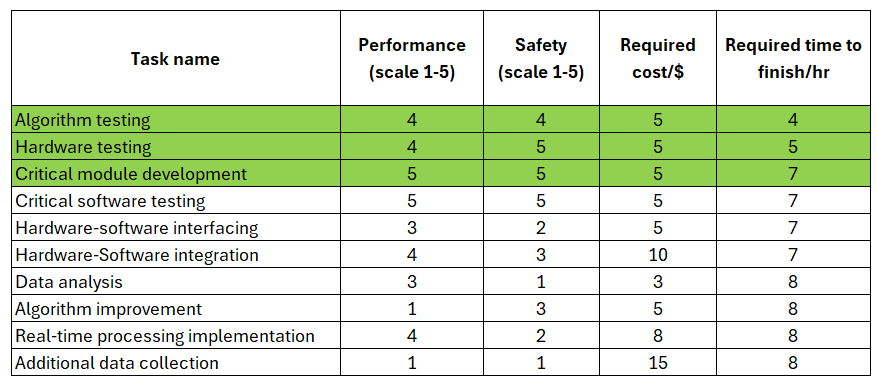
In table 5, the applied optimisation procedure is:

1. First, we sort in descending order (largest to smallest) the task based on “performance”.
2. Then, we re-sort again in descending order (largest to smallest) the task based on “safety”.
3. Then, we re-sort in ascending order (smallest to largest) the task based on “required cost”.
4. Then, we re-sort again in ascending order (smallest to largest) the task based on “required time to finish”.
5. Finally, we select the top tasks that can be finish within <24 hrs.

The selected task based on table 5 are: algorithm testing, hardware testing and critical module development.

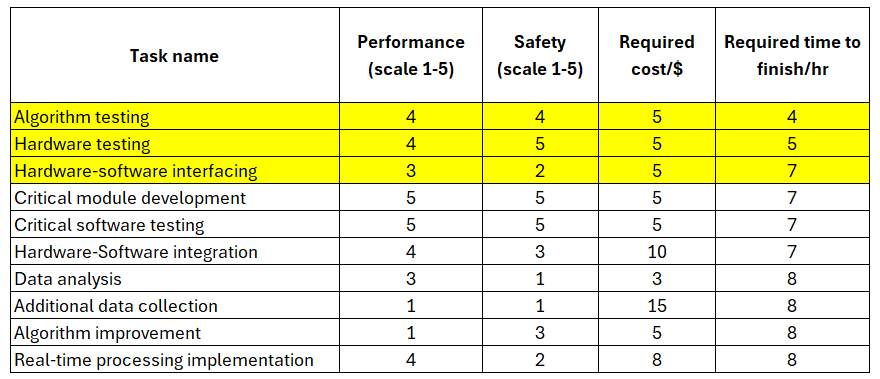
Meanwhile, table 6 shows the selected tasks when we directly sort based on the “required time to finish”.

Based on table 6, the selected tasks are algorithm testing, hardware testing and hardware-software interfacing.

Form table 5 and table 6, we can see that the selected tasks in table 5 prioritise tasks that have higher importance than the selected tasks in table 6.

READ MORE: Simplicity is the ultimate sophistication: The use of simple rules for successful research

Conclusion

We have presented a light but practical (and hopefully useful) post regarding how to select or prioritise tasks based on quantitative method.

The main goal is to select optimal task where we cover the most important tasks with minimum required resources to deliver as much value as possible within a given deadline. In addition, we also discuss a simple rule theory in defining the importance criteria of tasks.

The task-selection problem is modelled as “min-max” problem and a quantitative way to solve the problem (in this case task selections) has been presented.

Two examples have been presented to show the practicality of the method to optimally select important tasks while minimising required resources within a tight deadline.

 References

[1] Rardin, R.L. and Rardin, R.L., 1998. Optimization in operations research (Vol. 166). Upper Saddle River, NJ: Prentice Hall.

[2] Sull, D.N. and Eisenhardt, K.M., 2015. Simple rules: How to thrive in a complex world. Houghton Mifflin Harcourt.

You may find some interesting items by shopping here.