Error compensation for coordinate measuring instrument: Error separation and self-calibration
Rehearsal method is a method to separate combined or coupled errors into separated individual error elements. By separating the combined errors into individual errors, the error quantification of an instrument can be performed without a calibrated artefact and/or calibration instrument.
Rehearsal method is a method to separate combined or coupled errors into separated individual error elements. By separating the combined errors into individual errors, the error quantification of an instrument can be performed without a calibrated artefact and/or calibration instrument.
This method is categorised as “self-calibration” method.
One of the most famous self-calibration methods is rehearsal method. This rehearsal method performs several measurements with different artefact positions/orientations and/or motion stage positions/orientations and then separate the error of interest from other compounded errors, such as geometrical errors from a measured artefact.
At the end of this post, readers will understand about two basic rehearsal methods that have been commonly used in industries for self-calibration.

Rehearsal method for self-calibration process
In this section, the most basic rehearsal method is presented to easily and concretely explain about the concept of rehearsal method.
In principle, rehearsal methods (including self-calibration) require performing several measurements (minimum two measurements) by changing either the position of an instrument (under rehearsal process) or a reference calibrated artefact or both the instrument and the artifact.
The main requirement for artefact used for rehearsal process is that the artefact has a stable geometry (also known as rigid) with respect to variation in temperature, pressure, humidity and other environmental noises.
Two main rehearsal methods that will be discussed in this post are straightedge rehearsal and Donaldson rehearsal method [1].
READ MORE: Error compensation for coordinate measuring instrument: Steps and calibration instruments
Straightedge rehearsal method
Straightedge rehearsal method is used to measure the error of straightness of the axis of a motion stage without using a calibrated artefact or laser interferometer (as a common method to quantify straightness errors).
Figure 1 below shows the illustration of the straightedge method.
In figure 1, a motion stage, of which the straightness of its axis to be measured, is mounted by a dial gauge. Then, a straightedge, placed parallel with respect to the axis motion, is measured by the dial gauge.
Of course, the placement of the straightedge is not perfectly parallel to the axis motion. This imperfect parallelism causes a misalignment error and will add to the straightedge error of the motion stage.
In addition, there is also geometrical imperfections from the straightedge. Hence the total error read by the dial gauge is the straightness error of the motion stage, the misalignment error and the geometrical error of the straightedge.
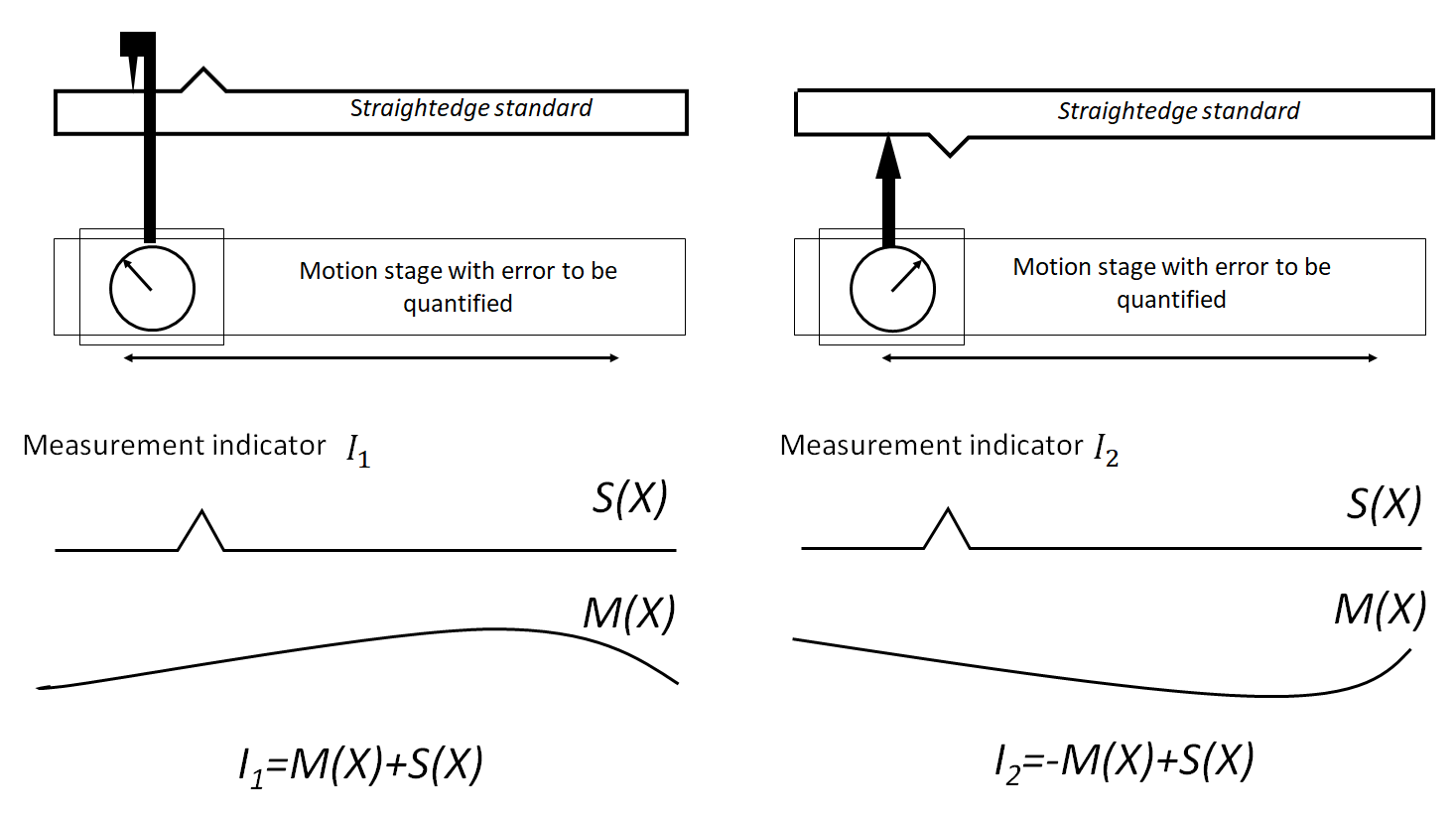
To separate the straightness error of the motion stage from the misalignment error of the set up and geometrical error of the straightedge, the rehearsal method is applied.
The procedure is as follows. after measuring the straightedge at one position (figure 1), the straightedge is rotated 180 degree (figure 1) and then remeasured by the dial gauge mounted on the motion stage.
In principle, the geometrical shape of the straightedge is the same (stable or rigid) whatever the positioning of the straightedge is.
If the straightness error of the motion stage is notated as $M(X)$, the geometrical error of the straightedge is notated as $S(X)$, the first dial gauge reading is $I_{1}$ and the second dial gauge reading is $I_{2}$. Hence, the straightness error of the motion stage can be separated and quantified as:
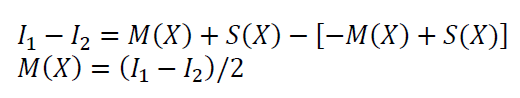
READ MORE: Error compensation for coordinate measuring instrument: introduction and types
Donaldson rehearsal method
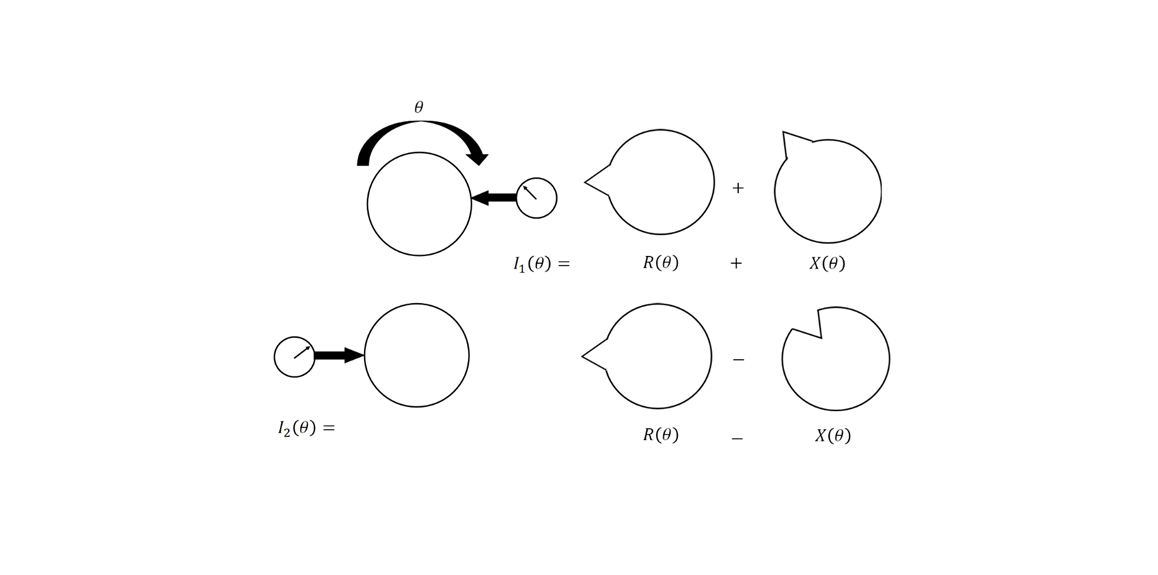
Donaldson rehearsal method is used to measure (quantify) the radial (roundness) error of a rotational motion stage.
Figure 2 below shows the illustration of the Donaldson rehearsal method. Donaldson method uses an uncalibrated sphere artefact to quantify the radial error of a rotational motion stage.
In figure 2, $X(\theta)$ is the radial error of a rotational motion, $R(\theta)$ is the roundness error of a sphere used for the rehearsal process and placed on the motion stage, $I_{1}(\theta)$ is the first dial gauge measurement and $I_{2}(\theta)$ is the second dial gauge measurement.
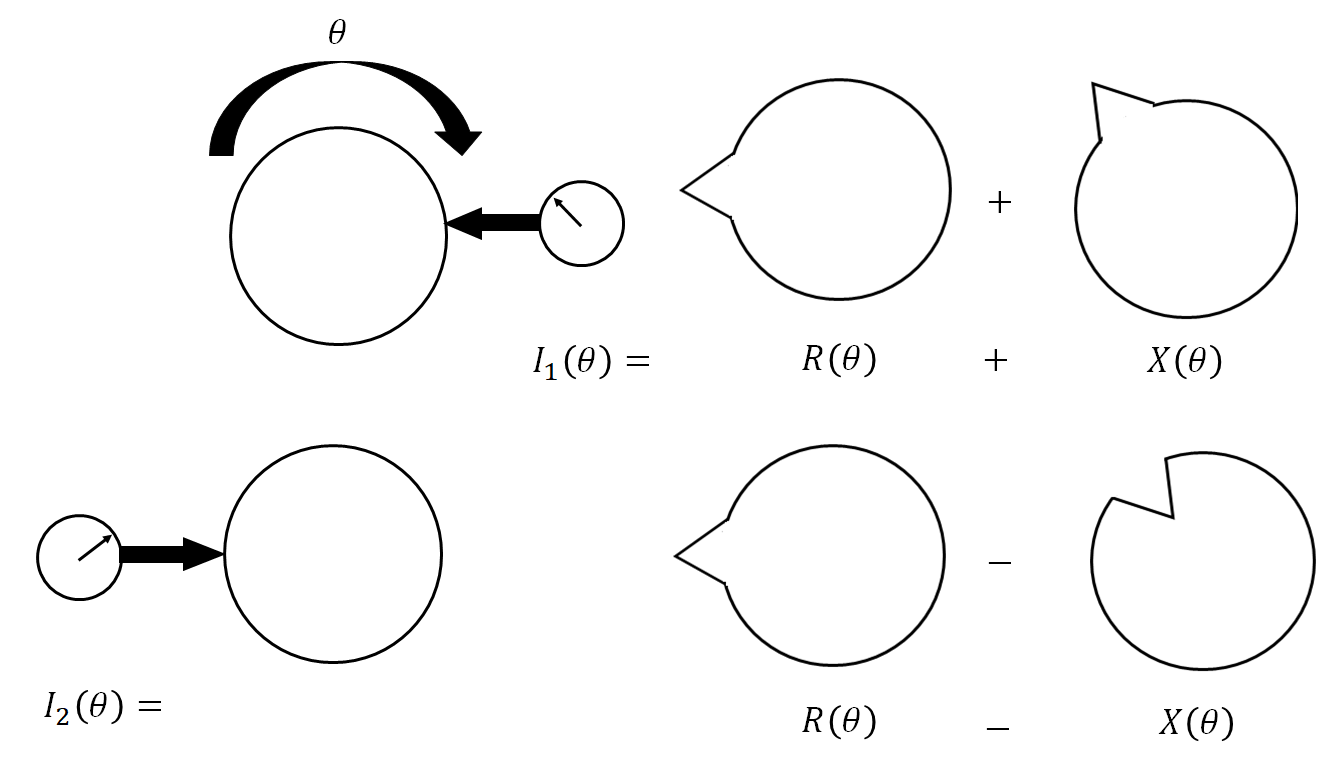
The Donaldson rehearsal method is performed as follows (see figure 2).
The roundness error of the sphere is measured by a dial gauge and by rotating the sphere about 360 degree. Then, the sphere is rotated about 180 degree from the sphere’s initial position on the motion stage and then the roundness error of the sphere is remeasured. Then, the sphere is rotated about 360 degree and the roundness is remeasured again by the same dial gauge.
After the rehearsal process, the radial error of the rotational motion stage is calculated as:
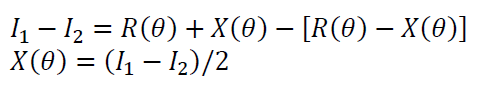
There are other types of rehearsal methods that are more complex than these two basics method. For example, the rehearsal method to quantify the 2D motion stage axis has been reported in [2]. Rehearsal method for 2D motion stage axis is very famous and has been implemented in industries.
READ MORE: Understanding measurement model, systematic error and random error
Conclusion
In this post, self-calibration processes by using rehearsal methods have been presented. The main idea of self-calibration (such as this rehearsal method) is to separate error of interest of a motion stage from other coupled errors, such as error from an artefact used for calibration, error form measuring instrument used for calibration, misalignment or setup error in calibration and other errors.
Two well-known rehearsal methods in industries have been presented and discussed. These two methods are straightedge rehearsal and Donaldson rehearsal methods.
Straightedge rehearsal method is used to quantify the straightness error of the axis of a motion stage. This rehearsal methods separated the straightness error of the motion stage and the errors from misalignment during setup and geometrical error of the straightedge used to quantify the straightness error.
Donaldson rehearsal method is used to quantify the radial error of a rotational motion stage. This rehearsal method used an uncalibrated sphere artefact. This sphere artefact is measured multiple times at different rotational positions by the rotational motion stage of which its radial error to be quantified. The radial error is then extracted from analysing the results of the multiple sphere measurements.
Reference
[1] Hocken, R.J. and Pereira, P.H. eds., 2016. Coordinate measuring machines and systems. CRC press.
[2] Ye, J., Takac, M., Berglund, C.N., Owen, G. and Pease, R.F., 1997. An exact algorithm for self-calibration of two-dimensional precision metrology stages. Precision Engineering, 20(1), pp.16-32.
You may find some interesting items by shopping here.
- TUTORIAL 3D tolerance stack-up analysis – A package containing PDF files, MATLAB scripts and CAD files that show in detail how to perform 3D tolerance analysis with a real case study.
