Metrology

Optical coordinate measuring machine (Optical-CMM): Two fundamental limitations

Optical coordinate measuring machines (Optical-CMM) have advantages over tactile (contact) CMMs, such as more part-feature accessibility, no surface damaging-risk and large surface points capture in relatively a short period of time (compared to tactile CMMs).

Wahyudin Syam

Jan 17, 2023 • 5 min read

However, all optical-CMM with objective lens and/or 2D imaging sensor have two fundamental limits. Those fundamental limits are numerical aperture limit and optical resolution limit.

In this post, we will discuss these two fundamental limits. At the end of this post, we will be aware of all optical-CMM limitations so that we can compare equally different optical-CMM instruments and can evaluate the basic performance of these instruments.

In addition, we can anticipate results that are non-valid for a specific optical-CMM instrument because the resolution of a feature to be measured is smaller than the lateral resolution of an optical instrument.

Let us dive into details!

Focus variation microscopy: performance and uncertainty evaluation- Dimensional and form measurements with optical CMMs

Numerical aperture limitation

Numerical aperture (NA) is a measure to assess the ability of an optical measuring instrument to measure the slope of a surface. Also, NA determines the optical resolution of optical instruments.

NA is a measure of how much light, that is reflected from a measured surface, can be collected and sent to imaging sensor for further processing.

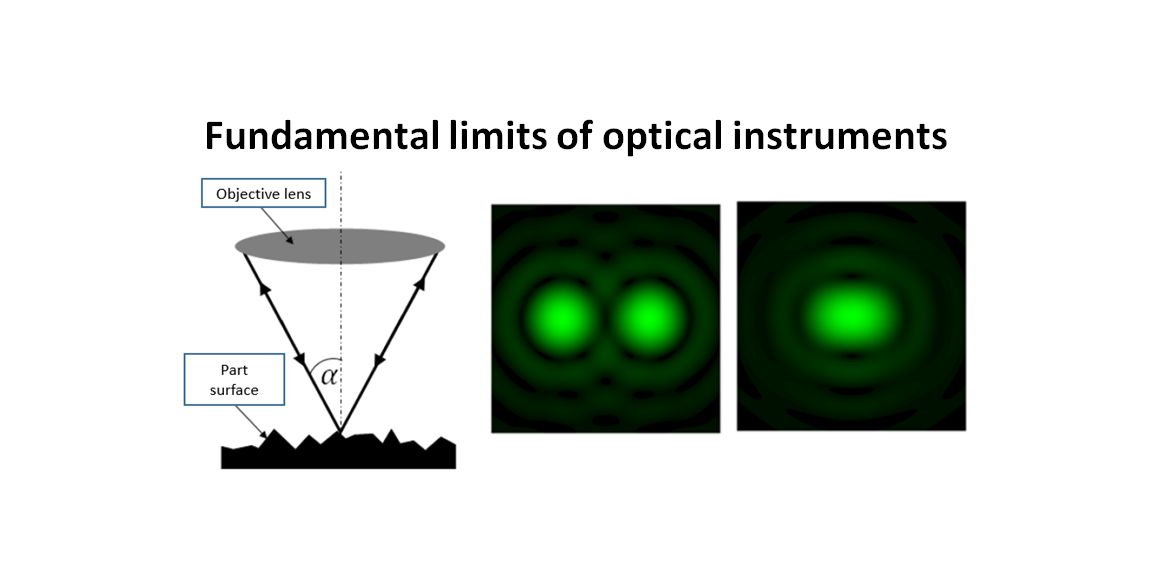
Figure 1 below shows the pictorial presentation of NA of an objective lens. From figure 1, NA is determined by how wide is the opening of an objective lens and the property of the medium where light travels, that is the medium bias index.

NA is formulated as:

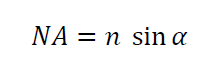
Where NA is numerical aperture, $n$ is the medium bias index where light travels and $\sin \alpha$ is the acceptance angle from an aperture or the opening of an objective lens.

Figure 1: Illustration of numerical aperture (NA) of an objective lens.

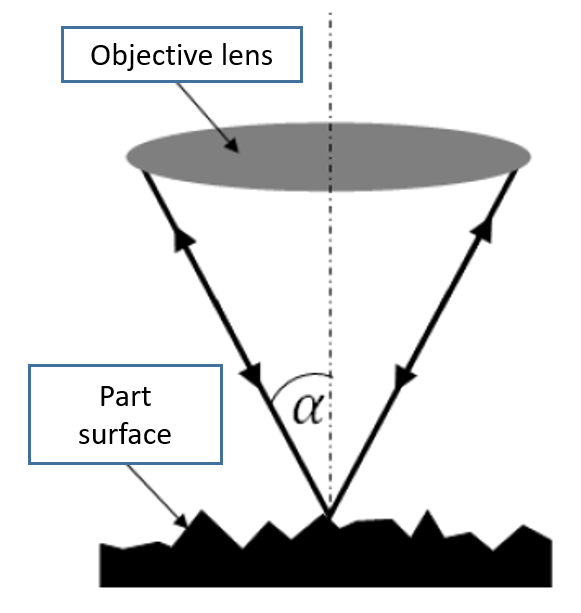
Figure 2 below shows the illustration of how large the slope of a measured surface that can still be measured by an objective lens with a specific NA. From figure 2, the larger the surface slope, the rougher the surface and the larger the NA of a required objective lens to measure.

Figure 2: Illustration of “surface slope” of a part surface.

Focus variation microscopy: performance and uncertainty evaluation- Dimensional and form measurements with optical CMMs

Optical resolution limitation (the limit of lateral X-Y resolution)

Lateral resolution is the minimum distance between two lateral (XY-direction) features on a measured surface that still can be measured by the instrument.

In other words, lateral resolution is the minimum lateral distance between two points such that these two points still can be differentiated between each other.

This lateral resolution of optical-CMMs is determined or limited by the optical resolution of the instruments when the optical resolution is larger than its pixel-distance.

Optical resolution (Rayleigh criterion) is formulated as:

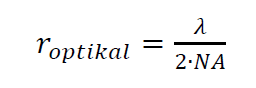
Where $r_{optical}$ is the optical resolution of a microscopy system (the minimum lateral resolution) and $\lambda$ is the wavelength of the light source use by the microscopy system (if the light contains multiple wavelength, hence the value is the mean wavelength).

For a microscopy system that uses 2D digital camera sensor, the lateral resolution of 5$\times$ and 10$\times$ objective lenses is limited by the pixel-distance. Because the pixel-distance on these objectives is larger than their optical resolution of the objective lenses.

Pixel-distance is calculated as:

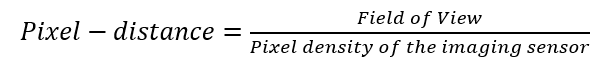
For 20$\times$ objective, the pixel distance is still a slightly larger than the optical resolution. Hence, the lateral resolution is limited by the pixel-distance on the 2D camera imaging.

However, for 50$\times$ objective lens, the optical resolution is larger than the pixel-distance. Hence, for this objective, the lateral resolution is limited by the optical resolution, instead of the pixel-distance.

Table 1 below shows comparisons between optical resolution and pixel-distance for difference magnification of objective lenses. From table 1, we can observe that for 50$\times$ objective lens, the lateral resolution is limited by the optical resolution instead of pixel-distance.

Table 1: Comparison of optical resolution and pixel-distance for various magnification of objective lenses.

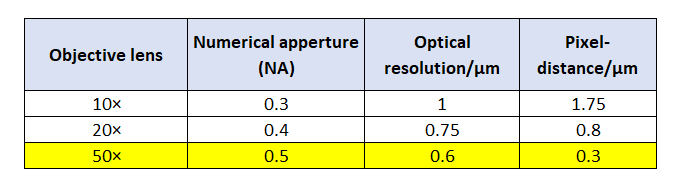
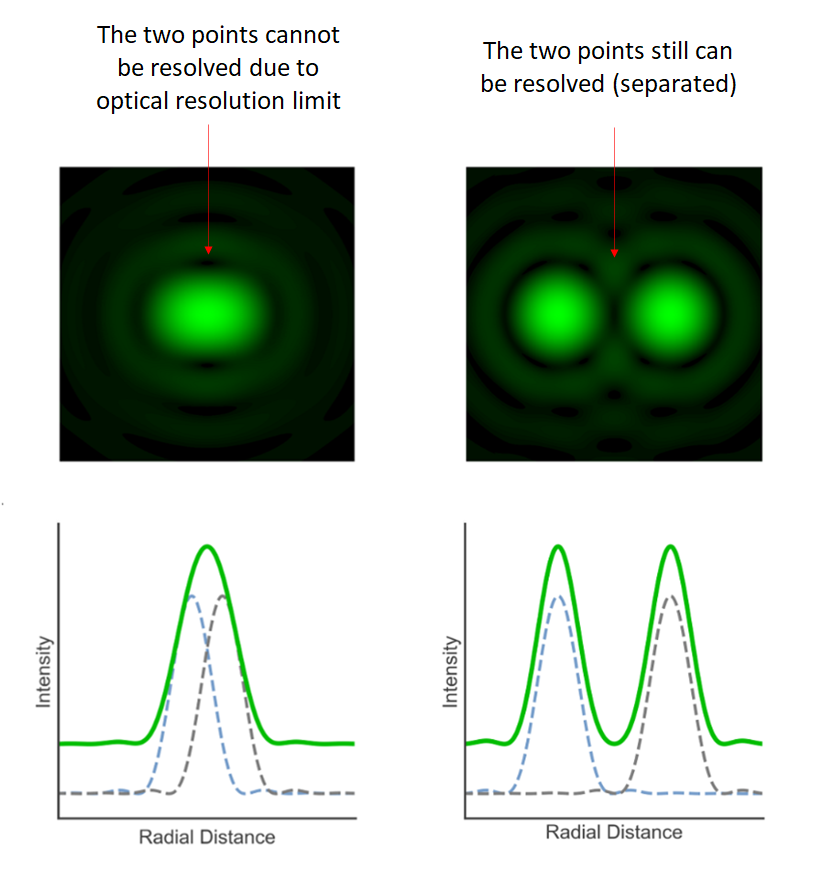
Figure 3 below shows the examples of lateral resolution of an optical instrument. From figure 3, if the lateral distance between two points are larger than the lateral resolution (either limited by pixel-distance or optical resolution), then the two points can be differentiated, and otherwise.

Hence, we need to be careful that an instrument cannot measure a feature that is smaller than its lateral resolution that is either limited by the pixel-distance or optical resolution.

Figure 3: Example of optical resolutions: (left) the two points are resolvable and (right) the two points are not resolvable (Source: https://www.edinst.com/blog/the-rayleigh-criterion-for-microscope-resolution/).

In addition, another importance factor that affects the lateral resolution of an optical instrument is the diameter of the focused spot of the light coming out from the objective lens. The size of the spot directly affects the size of the area that can be seen by the objective lens, that is it will affect the calculation of pixel-distance (see the pixel-distance equation above).

The diameter of the spot of focused light is formulated as:

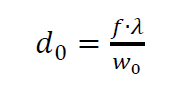
Where $d_{0}$ is the spot diameter of the focused light on a measured surface, $f$ the focal length of an objective lens, $\lambda$ is the wavelength of the light and $w_{0}$ is the beam waist, that is the radius from $\frac{1}{e^{2}}$ from the radiation contour on a plane when the wave front is flat.

Conclusion

In this post, two fundamental limitations of optical-CMM have been presented. These two fundamental limits are: numerical aperture limitation and optical resolution limitation.

The numerical aperture limitation determines the maximum slope angle that can be measured by an optical-CMM. It is important to remember that the larger the surface slope to measure, the rougher the surface will be and hence the larger the NA of an objective lens that is required to measure the surface.

Meanwhile, the optical resolution (when it is larger than the pixel-distance) of an objective lens determine the lateral resolution of optical-CMMs. This aspect is very important to understand because in many cases, lateral resolution is determined by the pixel-distance.

You may find some interesting items by shopping here.