Post-correlation Carrier to Noise Density (C/N0) calculation in GNSS signal processing

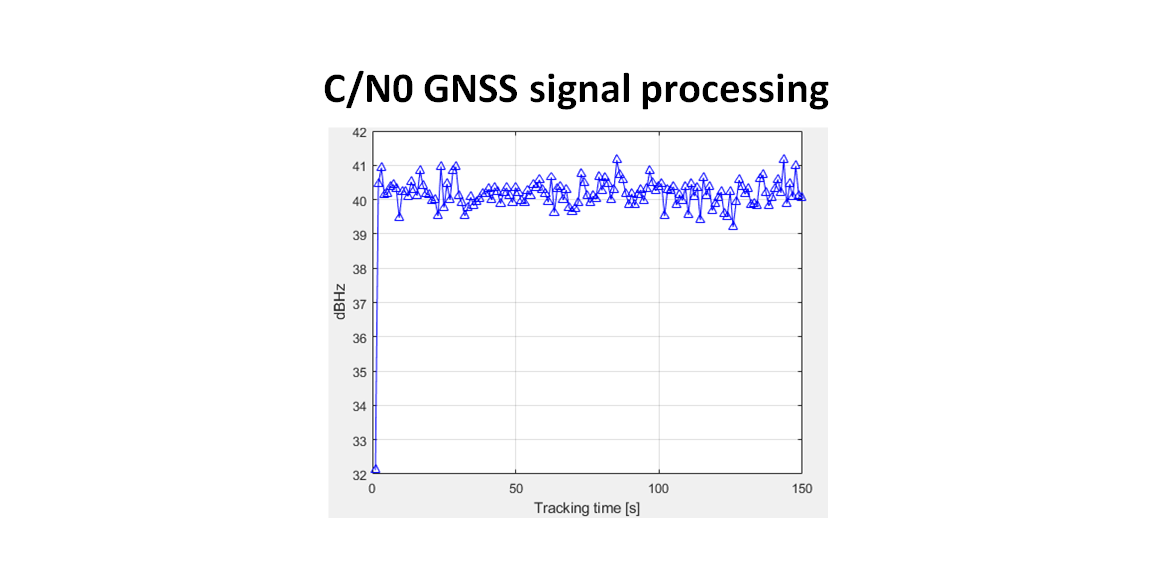
Carrier to Noise Density (C/N0) is one of instrumental metrics for GNSS receiver and signal processing. In this post, C/N0 is calculated at the post-correlation stage (signal tracking) in the GNSS signal processing stage [1].

This post correlation method for calculating C/N0 is the de facto method for GNSS receiver and signal processing.

Unlike the basic method (pre-correlation method), in this post correlation method, the calculation of C/N0 does not require the SNR information of the signal. Because, received GNSS signal at the front-end of a receiver is buried under noise. Hence, the SNR calculation will be ambiguous due to the noise power is above the signal power.

In addition, from reported studies [2][3], the C/N0 calculation using pre-correlation method will be overestimated if there are interferences concentrated around the centre of GNSS (in this case report is GPS signal) signal spectrum and will be underestimated if the interferences are concentrated at the edge of the signal spectrum.

In short, post-correlation C/N0 estimation is a better method than pre-correlation estimation.

In GNSS signal processing, the post-correlation C/N0 is the carrier power to noise density of prompt correlated symbols, that is the symbols are or part of the navigation data message and is expressed in dB-Hz.

Let us dive into the discussion!

READ MORE: The difference between C/N0 and SNR in GNSS signal processing

The importance of C/N0 estimation in GNSS signal processing

In GNSS signal processing, the calculation of C/N0 is very critical. Because, the C/N0 value is used to determine whether the code and carrier tracking loops are in lock, to predict the performance of a GNSS receiver and/or its software receiver.

In addition, C/N0 value can be useful to adjust the software receiver responses (DLL and PLL loop) in low signal to noise environments.

It is very common that a GNSS receiver and software processing works in low signal to noise environments.

The reasons are:

• Firstly and foremost, received GNSS signal themselves are very weak (typically -128 dBm).
• Secondly, environment disturbances, such as intentional and/or unintentional interferences, cause the GNSS signal power (C/N0) to be smaller compared to noise.

Examples of unintentional interference are multipath due to reflection from surroundings (such as city or dense urban area and inside buildings) and other signal close to GNSS signal frequency, such as mobile satellite services, broadcast television and other wideband communication systems.

Examples of intentional interference are jamming and spoofing. These intentional interferences are considered as attack to GNSS signal and should be mitigated. Jamming attack commonly causes GNSS signal become unavailable or degraded. Meanwhile, spoofing attack commonly causes a receiver to be fooled so that the receiver provides invalid or wrong PNT solutions.

Pre-correlation method for C/N0 calculation are very noisy for low signal to noise environments. Hence, this noisy C/N0 can cause problems to determine whether code and carrier tracking are in lock or not.

Invalid decision can be obtained: loss of lock falsely declared when a signal is being tracked perfectly well or lock declared when a signal lock has been lost (that is, the tracking error is outside the correlator window).

READ MORE: GNSS signal modelling considering channel impairments and spoofing interferences

The methods to calculate C/N0 in GNSS signal processing

There are at least three methods to calculate C/N0 in GNSS signal processing:

• Narrow to wide band power ratio method
• Correlator comparison method
• Discriminator output statistics method

Based on a study in [1], all of the above methods are effective including in low signal to noise environment. However, the narrow to wide band power ration method has been reported to perform better in terms of noise (lower variation) in low signal to noise environments [1].

The Narrow to wide power ratio method is the most used post-correlation C/N0 calculation in GNSS signal processing.

Narrow to wide band power ratio method: the derivation

The derivation of the C/N0 calculation by narrow to wide band power ratio method is explained as follows.

The narrow band $P_{N}$ and wide band $P_{W}$ power are calculated as:

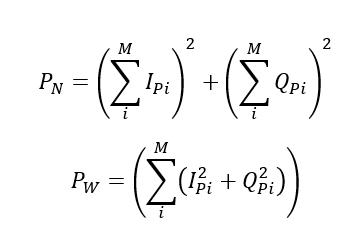
Hence, the power ratio between narrow and wide band is calculated as:

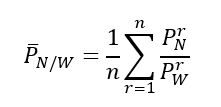
Note that the equation above to calculate the power ratio is averaged over $n$ iterations to reduce noise.

The estimated C/N0 is from the expected value of the average power ratio. The expected value of the power ratio is then calculated as:

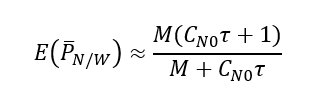
Where $\tau$ is the accumulation interval that is divided over $M$ intervals.

By re-arranging the expected value equation above, the estimated C/N0 is then calculated as:

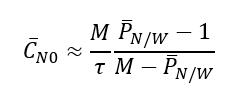
In addition, the standard deviation of the estimated C/No is:

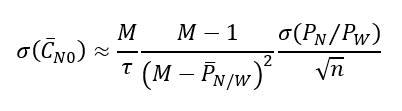
Narrow to wide band power ratio method: the calculation procedure

In summary, for the implementation of the C/N0 calculation in a program, the C/N0 calculation procedure using the narrow to wide band power ration method is as follows [4]:

• Calculate the narrow band ($NBP$) and wide band ($WBP$) powers as:

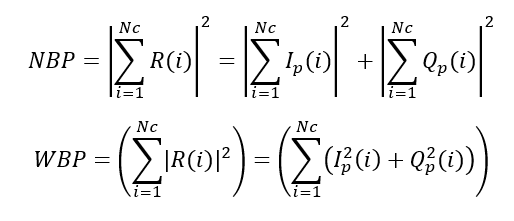
Where $R(i)$ is the complex prompt correlator output for both I ($I_{p}$) and Q ($Q_{p}$) signal and $N_{c}$ corresponds to the number of correlators (usually 20 for GPS, since 1 symbol is 20 ms = 20 PRN cycle)

• Calculate the narrow to wide band power ratio $NP$ as:

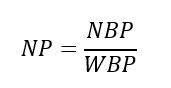
• Finally, calculate the C/N0 (in dB-Hz) as:

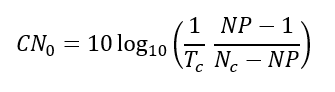
Where $T_{c}$ corresponds to the coherent integration time in second ($0.001 s$ for GPS and $0.004 s$ for Galileo).

Note that the procedure above is ready to be implemented in any programming languages.

READ MORE: The difference between C/N0 and SNR in GNSS signal processing

Conclusion

In this post, a post-correlation method to calculate the C/N0 of GNSS signals has been presented. The post-correlation method is the ration between narrow and wide band power. The post correlation method for calculating C/N0 is the de facto method for GNSS receiver and signal processing.

The estimation of signal C/N0 is instrumental for determining whether the code and carrier tracking loop in GNSS signal processing is in lock, determining the SNR of GSNSS signal to assess the performance of a receiver and responding and adjusting the signal GNSS tracking process to low SNR conditions.

The main advantage of post-correlation methods to calculate C/N0 over pre-correlation are the C/No estimation is robust with respect to signal interferences either concentrated at around the centre of at the edges of the signal spectrum.

The main advantage of narrow to wide band power ratio post-correlation method over the other two post-correlation methods are this power ratio method has less variation in weak GNSS signal condition (high noise environment, such as multipath and other interferences).

Finally, the detailed procedure to calculate C/N0 in the signal tracking (post-correlation) stage is presented and can be directly implemented in any procedural or functional programming languages.

References

[1] GPS Signal‐to‐Noise Measurement in Weak Signal and High‐Interference Environments. Navigation

[2] Betz, J.W., 2001, January. Effect of partial-band interference on receiver estimation of C/N0: Theory. In Proceedings of the 2001 National Technical Meeting of the Institute of Navigation (pp. 817-828).

[3] Ross, J.T., Leva, J.L. and Yoder, S., 2001, January. Effect of partial-band interference on receiver estimation of C/N0: measurements. In Proceedings of the 2001 National Technical Meeting of The Institute of Navigation (pp. 829-838).

[4] Seco-Granados, G., Gómez-Casco, D., López-Salcedo, J.A. and Fernández-Hernández, I., 2021. Detection of replay attacks to GNSS based on partial correlations and authentication data unpredictability. Gps Solutions, 25(2), p.33.

You may find some interesting items by shopping here.