The difference between C/N0 and SNR in GNSS signal processing

In signal processing, especially in global navigation satellite system (GNSS), the term signal-to-noise ratio (SNR) and carrier-to-noise density (C/N0) are very fundamental in every analysis aspect.

These values are very often used to analysing, processing and understanding signals, especially for radio frequency (RF) signals. However, these two terms are very often interchangeably used as if they are the same.

In fact, these two terms are fundamentally different and can explain different things about a signal.

In this post, we will clearly define the difference between SNR and C/N0 in term of their definitions, their units, their application, their use and other aspects. It is very useful to understand the differences between C/N0 and SNR for GNSS community (system designer, user, tester, developer, receiver designer, and others).

One important note is that both SNR and C/N0 are important parameters in analysing RF signals. And, many times, these two parameters are both calculated to give a comprehensive description about RF signals.

The main used for both SNR and C/N0 parameters are to indicate the strength of GNSS signals.

READ MORE: GPS (GNSS) signal processing chain from a received raw signal, signal acquisition, tracking to demodulation: An introduction

Signal-to-Noise Ratio (SNR)

The definition, property and application of SNR are as follow:

• SNR is the ratio between the power of a signal or carrier and the power of noise in a given specific bandwidth. Hence, when we say about SNR, we should also mention the bandwidth that we use to calculate the SNR.
• SNR is expressed in decibels (dB) or decibel milliwatt (dBm) or sometimes decibel Watt (dBW).
• SNR formula:

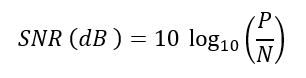
Where $P$ and $N$ can be unitless or in $mW$ or $W$.

SNR can also be calculated as:

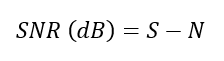
Where $S$ is the signal or carrier power in dB or dBm or dBW and $N$ is the noise power in a given bandwidth in dB or dBm or dBW.

The main use or application of SNR

• SNR is bandwidth-dependent. Hence, we need to have the same bandwidth to have a fair SNR comparison between different signals.
• SNR is also dependent to algorithm and processing stages of receiver algorithms. Hence, to compare SNR, we need to specify the bandwidth and the processing stage.
• SNR can be used to compare the acquisition and tracking algorithms in GNSS software receivers.
• SNR can be used as an indicator of the noise presence in a measurement.
• SNR can be used in Monte-Carlo analysis of signal simulations. In signal simulations, the noise variance of the signal is derived from the SNR. In case we have C/N0 in our simulation data, we need to convert the C/N0 into SNR so that we can estimate the noise variance in the simulation.

READ MORE: Beware of reading signal-to-noise ratio (SNR) from power spectral density (PSD) plot

• Global Positioning System: Signals, Measurements, and Performance - an excellent GPS and GNSS book for modelling

Carrier-to-Noise Density (C/N0)

The definition, property and application of C/N0 are as follow:

• C/N0 is the ratio between a carrier power and the power of noise per unit bandwidth. C/N0 is commonly calculated using Welch’s algorithm (the algorithm to calculate the power spectral density or PSD of a signal).
• C/N0 is expressed in decibel-Hertz (dB-Hz).
• C/N0 formula:

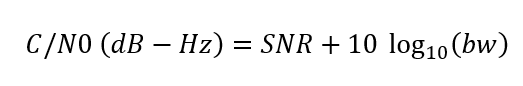
Or

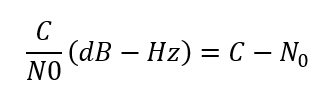
Or

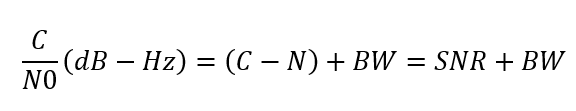
Where $bw$ is the front-end bandwidth in Hz, $BW=10 log(bw)$, C is the carrier power in dB or dBm or dBW and N is the noise power in dB or dBm or dBW

The main use or application of C/N0

• C/N0 is independent from the receiver bandwidth (in practice). Hence, can be used for comparison of various receiver or software receiver.
• C/N0 can be directly used to indicate the quality of a received signal.
• C/N0 provides an indication of the signal strength of a tracked satellites and, also, the noise density of the receiver front-end.
• C/No provides an indication of the quality of a signal and is independent to acquisition and tracking algorithms used by different receivers.

READ MORE: The problematic aspect of number crunching in programming: Case study in GNSS calculations

A quick look for SNR and C/N0 for GPS L1 C/A signal

The thermal noise of an antenna and receiver hardware can be used to specify noise density and is calculated as:

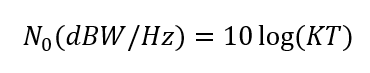
Where $K$ is the Boltzmann’s contant = $1.38 \times 10^{-23} J/K$, $T$ is the noise temperature in Kelvin, typically 290 K.

Hence, the noise density of a common noise from a receiver temperature is:

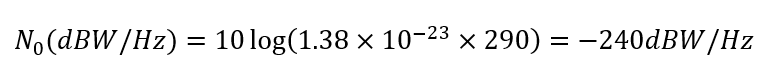
A typical carrier power $C$ of a GPS L1 C/A signal at a receiver is about -158.5 dBW.

Hence, a typical nominal C/N0 on a GPS receiver is $C/N0 = C-N_{0}=-204+158.5=45.5 dB-Hz$.

Assuming we use sampling rate of 10 MHz with a RF front-end. We can calculate BW as $10log(10^{6})=70dB$

Hence, from the C/N0, we can calculate the SNR as: $SNR=C/N0-BW=45.5-70=-24.5 dB$.

That is the SNR value is negative at a receiver front-end.

READ MORE: Generating GPS L1 C/A pseudo-random noise (PRN) code with MATLAB and C/C++

Conclusion

In this post, we have presented the difference between SNR and C/N0. Although both of these parameters represent the strength of a signal, but both of them have different definitions and lead to a different understanding of a signal.

One important note is that both SNR and C/N0 have the same importance in signal analysis and very often both of these parameters are used together to get a comprehensive view of signal analysis. Their use in signal analysis depends on the context and/or purpose of the analysis.

By knowing the difference, we can get a better information or accurate information from their numbers toward our signal under analysis. Also, we can communicate with peers about a signal without any misunderstandings.

You may find some interesting items by shopping here.